Collatz Conjecture

The Collatz Conjecture, also known as the $3n + 1$ conjecture, is a mathematical problem that has puzzled mathematicians for decades. It was first proposed by the German mathematician Lothar Collatz in 1937. The conjecture states that for any positive integer $n$, the sequence generated by repeatedly applying the function:

$$f(n) = \begin{cases} n/2 & n \text{ even} \\ 3n+1 & n \text{ odd} \end{cases}$$

will always reach 1 regardless of the value of $n$.

Another way to think about it is that starting with 1, all positive numbers will be reachable by repeatedly applying the function in reverse:

The conjecture has been tested for many starting values of n, and it has been found to be true for all integers up to $5 * 10^{18}$. Despite this, no one has been able to prove or disprove the conjecture for all positive integers.

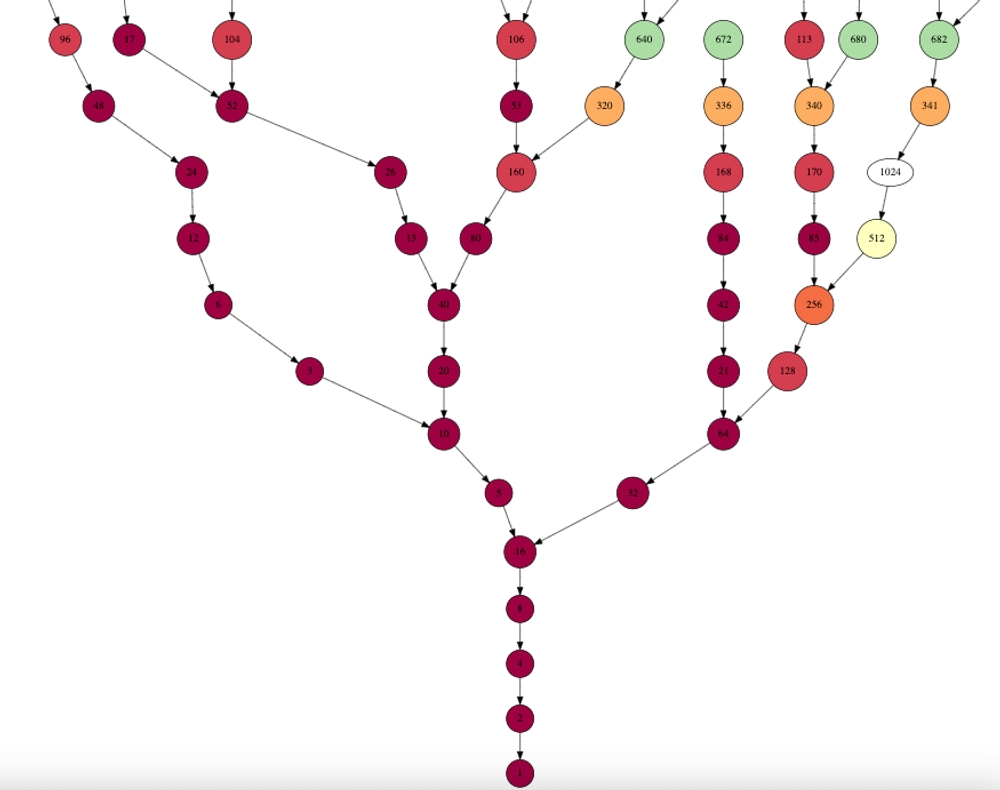
Many mathematicians have attempted to prove the conjecture, but so far all attempts have failed. Some have tried to prove it by contradiction, assuming that the conjecture is false and then showing that this leads to a contradiction. Others have tried to prove it by finding a pattern in the sequence, but no such pattern has been found. Take a look at the following picture for some sequences

Mathematics may not be ready for such problems. - Paul Erdős

The problem is also known as the hailstone problem because the sequence generated by the collatz conjecture fluctuates up and down like hailstones in a storm and they always end up on the ground.

If you want to dive deeper into the collatz conjecture you can read the amazing book The Ultimate Challenge: The 3x 1 Problem by Jeffrey C. Lagarias.